Elastic Net: An Intuitive Explanation

Elastic net is a proper tool when we have lots of correlated features in regression.

Major Lessons

In this scenario, if you apply the vanilla LASSO the resulted coefficients are not stable. Instability here means that if you decrease the \(\lambda_t\), the regularization parameter, by \(t\) for each \(\lambda_t\) in the path of the LASSO the value of non-zero coefficients can change substantially in any direction (increase/decrease). So depending on the chosen \(\lambda\) the value of regression coefficient \(\beta_i\) (that determines the importance of the feature \(X_i\) ) can be drastically different and we don’t have any idea of the relative significance of features.

In a non-degenerate scenario of applying the LASSO, you would hope that after the initial selection of a feature in the LASSO path, its coefficient escapes shrinkage gradually when \(\lambda_t\) decreases and reaches the OLS value.

Such an eventual increase/decrease in selected coefficients does not happen in the correlated features case because those features, arbitrarily divide the importance weight, i.e., coefficients, among themselves while it should be almost uniformly distributed among the correlated dimensions.

The uniformness of coefficient over the correlated features can be induced using \(l_2\) penalty (why?). Therefore, elastic net suggests a convex combination of both \(l_1\) and \(l_2\) penalties:
\(\begin{aligned} \hat{\beta} &\in \mathop{\mathrm{argmin}}\limits_{\beta} \frac{1}{n} \|\mathbf{y}- \mathbf{X}\beta\|_{2} + \lambda \left[\alpha \|\beta\|_{1} + (1-\alpha) \|\beta\|_{2}^2 \right] \\ \end{aligned}\)

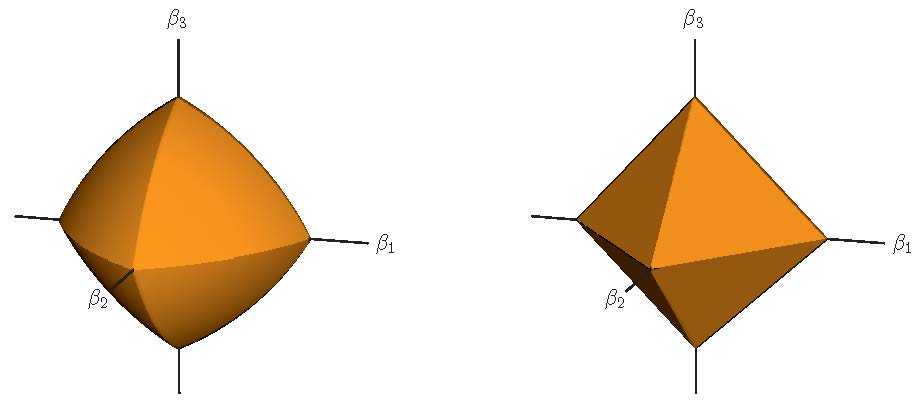
Interestingly, the resulted norm ball has sparse facets like \(l_1\)-norm ball while each facet is curved, encouraging equal values for the selected features on that facet.

Below is the elastic-net ball with \(\alpha = 0.7\) (left panel) in \(R^3\), compared to the
\(l_1\)-ball (right panel). The curved contours encourage strongly correlated variables to share coefficients. Image is from Statistical Learning with Sparsity The Lasso and Generalizations.